Cohen's kappa

Introduction

Cohen's kappa coefficient the amount measure the agreement between two classifiers, like other evaulation metrics, it is a handy tool to evaluate models, it is defined by this formula 👇

$$k\ =\frac{p_{0} -p_{e}}{1-p_{e}}$$

$$p_{0}\ = \ Probability \ of \ agreement \ , \ p_{e}\ = \ Hypothetical \ probability \ of \ chance \ agreement$$

This doesn't make a lot of sense, let us understand this better with an example.

The example

Two machine learning models as admissions officers at a University are going through a list of 100 candidates, who were applying for a grant and it was their decision to accept or decline it.

This is what the results look like 👇

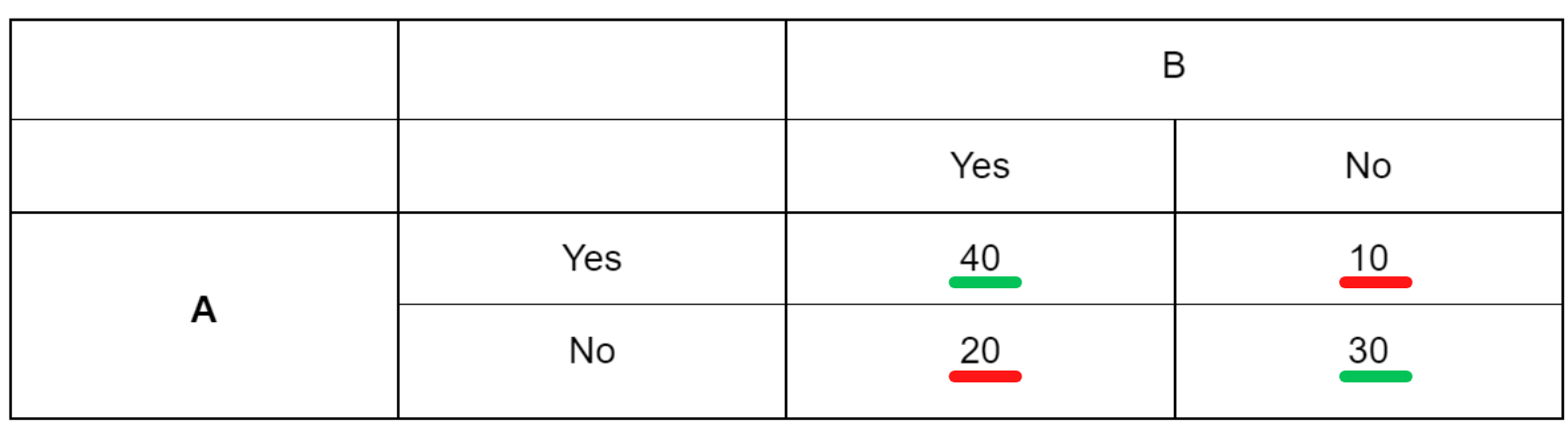
The cases underlined in green are where the admissions officers agree, the red indicates where they don't.

Let's apply the formula that we had before, starting by finding out P₀, the probabilty where the 2 admissions officers agree.

P₀

$$p_{0}\ =\frac{Cases \ where \ they \ agree}{Total \ number \ of \ cases}$$

$$p_{0}\ =\frac{40 + 30}{100}$$

$$p_{0}\ =\frac{70}{100}$$

P₀ = 0.7 or 70%, what this means is that probabilty that the officers agree is 70%, 7 out of 10 times their decision whether to give a candidate the grant will be the same.

P_e

Now let's calculate P_e, the probability of random agreement.

Admission's officer 'A' says yes to a candidate 50 out of 100 times, therefore the probabilty that A says yes is 0.5, on the other hand the probability that officer 'B' says yes is 0.6 by this simple calculation.

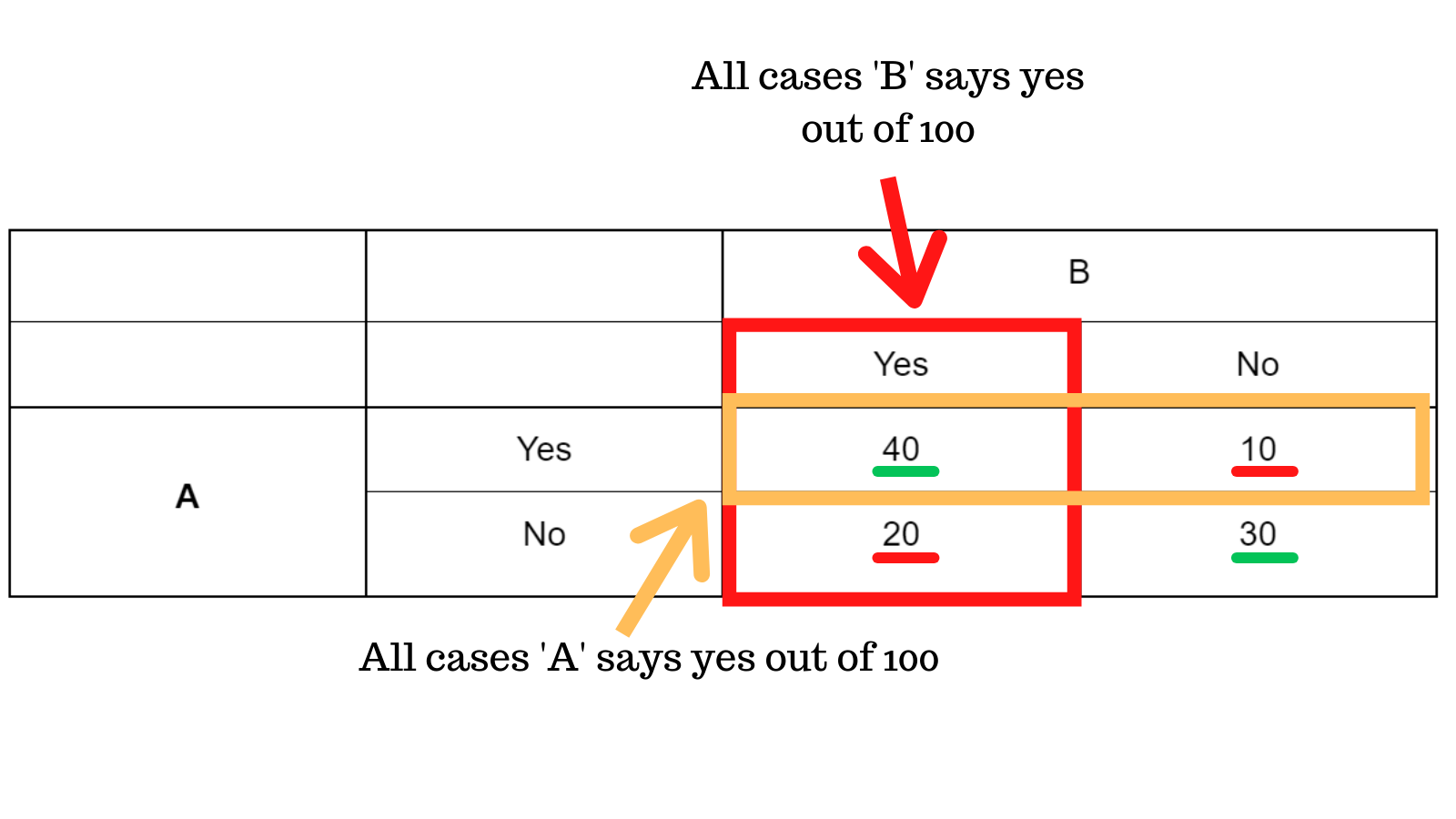
This means that the probability of them both randomly saying yes = 0.5 x 0.6 = 0.3

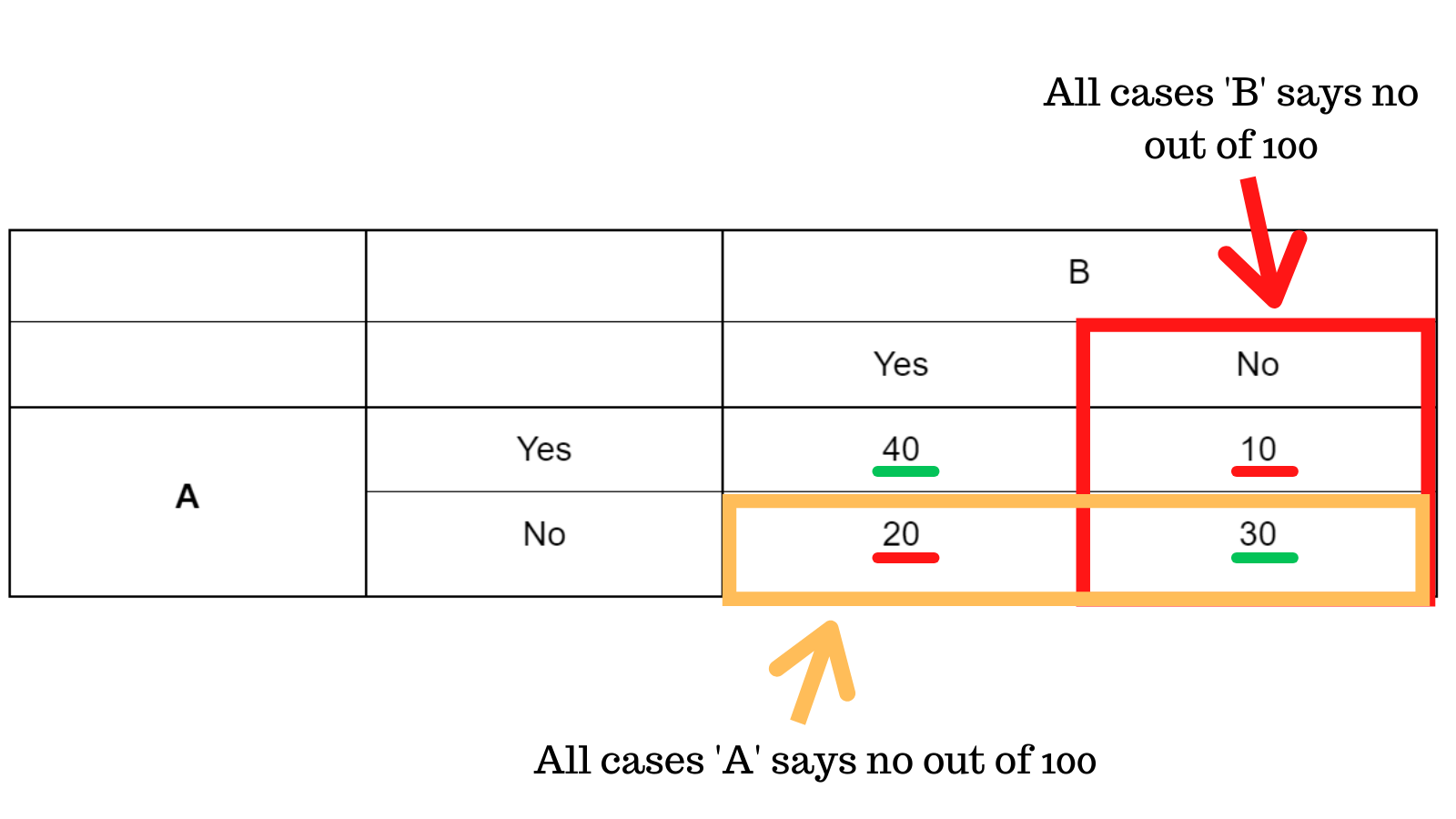
Similarly, applying this in the other case, A says no with a probability of = 0.5 and B with 0.4 which equates 0.5 x 0.4 = 0.2

P₀ = 0.7 , P_e = 0.2

Finally, calculating Cohen's Kappa.

$$k\ =\frac{0.7 \ - \ 0.2}{1- 0.2} =\frac{0.5}{0.8} = 0.625$$

Interpretation

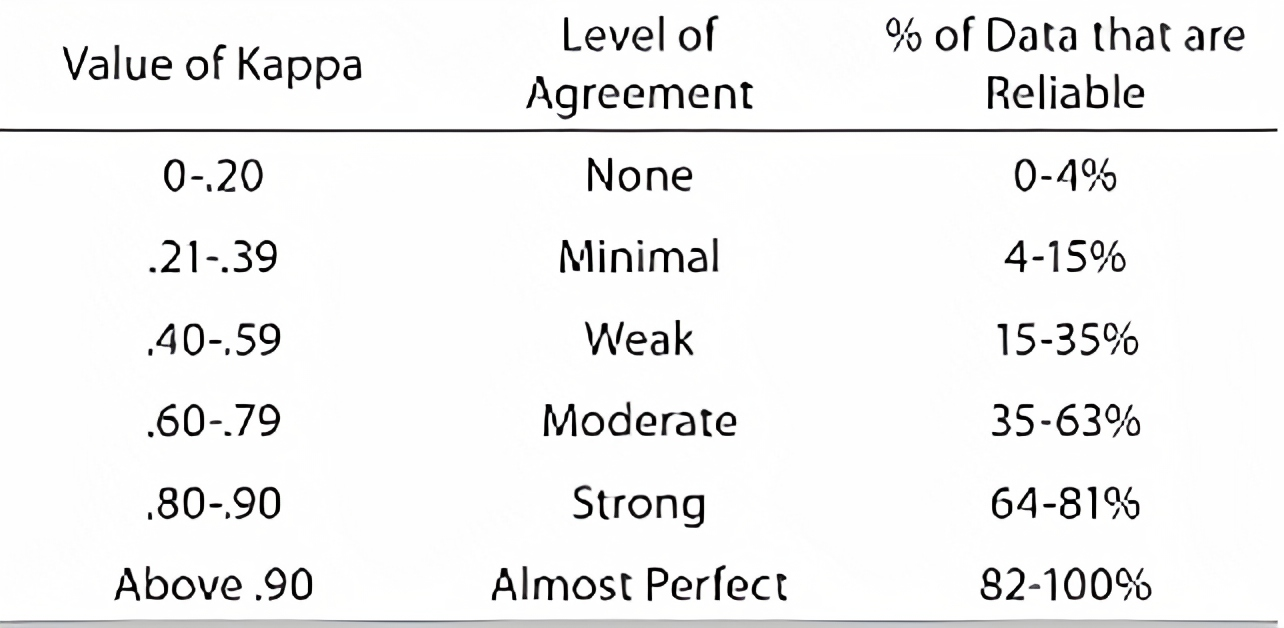
Cohen's kappa is generally used to determine the reliability of data in a dataset, this table is a general rule of thumb that co-relates to the Cohen's Kappa.

It essentially measures how much two models agree with each other.